Sac Bükme Makinasının Serbest Bükme Sırasında Bükme Kuvvetinin Hesaplanması

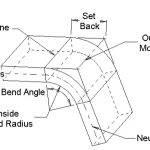
Son yıllarda metal fren bükme makineleri çeşitli endüstrilerde yaygın olarak kullanılmaktadır ve bükme makinelerinin işleme aralığı genişlemektedir. Ancak eğilme kuvvetinin hesaplanması konusunda sistematik bir tartışma yapılmamıştır. Şu anda, çeşitli abkant pres bükme makinesi üreticilerinin kılavuzlarında önerilen kabaca iki tür bükme kuvveti hesaplama formülü vardır.

P - bükme kuvveti, KN;

S - sac kalınlığı, mm;

l - levhanın bükülme uzunluğu, m;

V - alt kalıp açıklığının genişliği, mm;

σb - Malzemenin çekme mukavemeti, MPa.

Üretici tarafından önerilen bükme kuvveti parametre tablosu da yukarıdaki formüle göre hesaplanmıştır.

Eğilme kuvveti hesaplama formülünün türetme süreci ve uygulama kapsamı

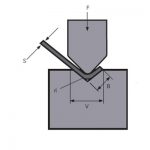
Şekil 1, sac bükme sırasında yapılan işin şematik bir diyagramıdır. Aşağıda, bükme kuvveti hesaplama formülünün türetme süreci ve iki ek parametre koşulu açıklanmaktadır. İlk olarak, ürün kılavuzunda bu tür öneriler var. Serbest bükmede, seçilen alt kalıp açıklığı genişliği V, sac kalınlığının S 8 ila 10 katıdır. Burada en boy oranını alıyoruz.

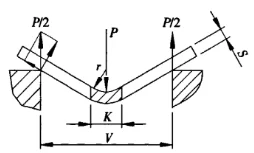
Şekil 1 Bükmenin şematik diyagramı

P - bükme kuvveti

S - sac kalınlığı

V - alt kalıp açma genişliği

r - levha büküldüğünde iç yarıçap

K - bükülme deformasyon bölgesinin yatay izdüşümünün genişliği=9

İkinci olarak, üretici, bükme kuvveti parametre tablosunda kalıp genişliği V ve bükme iş parçasının iç çapının r karşılık gelen değerlerini listeler. Genellikle r=(0.16~0.17)V. Burada çap-genişlik oranı =0.16.

Sac metalin bükülme işlemi sırasında, deformasyon bölgesindeki malzeme oldukça plastik bir deformasyon durumundadır ve merkez çizgisi etrafında bir açıyla bükülür. Bükülme bölgesinin dış yüzeyinde bazı durumlarda mikro çatlaklar görünebilir. Deformasyon bölgesinin kesitinde, merkezi tabakanın çevresi hariç, diğer noktalardaki gerilmeler malzemenin çekme dayanımına yakındır. Nötr tabakanın üst kısmı sıkıştırılır ve alt kısmı gerilir. Şekil 2, deformasyon bölgesindeki bir enine kesiti ve karşılık gelen stres diyagramını göstermektedir.

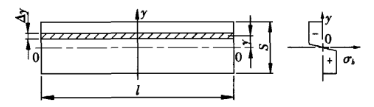
Şekil 2 Gerilme diyagramı

S - sac kalınlığı

l - sac bükme uzunluğu

Deformasyon bölgesinin enine kesitindeki eğilme momenti:

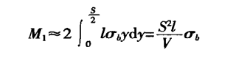
Deformasyon bölgesinde makinenin eğilme kuvveti tarafından üretilen eğilme momenti (bkz. Şekil 1):

İtibaren

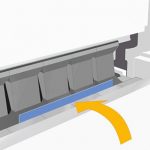
Bir bükme makinesinde serbest bükme için genel amaçlı kalıplar kullanıldığında, sac metalin çoğu 90° bükülür. Şekil 3'te gösterildiği gibi K:

K'yi denklem (1)'de yerine koyarsak, şunu elde ederiz:

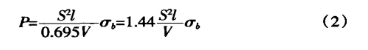
Sıradan malzemelerin gerilme mukavemeti σb=450N/mm2, formül (2)'yi şu şekilde değiştirir:

Türetme işleminden görülebilir ki, bükme kuvvetini hesaplamak için denklem (2) veya denklem (3) kullanıldığında, iki ek

yukarıda belirtilen parametre koşullarının karşılanması gerekir. Yani, en boy oranı=9, çap-genişlik oranı=0.16, aksi takdirde büyük bir hataya neden olur.

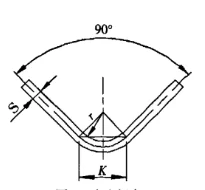
Şekil 3 Serbest bükme

S - sac kalınlığı

r - levha büküldüğünde iç yarıçap

K - bükülme deformasyon bölgesinin yatay izdüşümünün genişliği

Bükme kuvvetini hesaplamak için yeni yöntemler ve adımlar

Tasarım veya süreç gereksinimleri nedeniyle, yukarıdaki iki ek gereksinimi aynı anda karşılamak bazen zordur. Bu sırada önerilen hesaplama formülü eğilme kuvvetinin hesaplanmasında kullanılmamalı, aşağıdaki adımlara göre yapılmalıdır.

(1) Levha kalınlığı S, bükülme yarıçapı r ve alt kalıp açıklığı V'ye göre genişlik-kalınlık oranı ve çap-genişlik oranı sırasıyla hesaplanır.

(2) Sac deformasyonuna göre deformasyon bölgesinin izdüşüm genişliğini hesaplayın.

(3) Bükme kuvvetini hesaplamak için formül (1)'i uygulayın.

Hesaplama işleminde bükülme yarıçapının farkı ve buna karşılık gelen deformasyon bölgesinin değişimi dikkate alınmıştır. Bundan hesaplanan bükme kuvveti, genellikle önerilen formülle hesaplanan sonuçtan daha doğru ve güvenilirdir. Şimdi, Şekil 4'te gösterildiği gibi açıklamak için bir örnek verin.

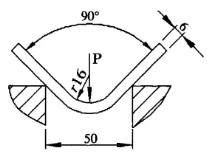
Şekil 4 Yeni hesaplama yöntemi

Bilinen: Sac kalınlığı S=6mm, sac uzunluğu l=4m, bükülme yarıçapı r=16mm, alt kalıp açıklığı genişliği V=50mm ve malzeme çekme mukavemeti σb=450N/mm2. Serbest bükme için gerekli bükme kuvvetini bulun.

İlk olarak, en boy oranını ve çap-genişlik oranını bulun:

İkinci olarak, deformasyon bölgesinin izdüşüm genişliğini hesaplayın:

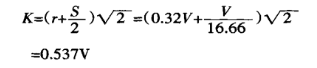
Son olarak, bükme kuvvetini bulmak için denklem (1)'i kullanın:

Eğilme kuvvetini hesaplamak için genel olarak önerilen formül kullanılırsa:

İtibaren = 1.5, ikisi arasındaki farkın 1.5 katı olduğu görülebilir. Bu hatanın nedeni, bu örnekteki bükülme yarıçapının nispeten büyük olması ve karşılık gelen deformasyon alanının artması, dolayısıyla bükme sırasında daha büyük bir bükme kuvvetinin gerekli olmasıdır. Bu örnekte, yukarıda tanıtılan parametrelerin ek koşullarını aşan çap-genişlik oranı = 0.32. Bükme kuvvetini hesaplamak için genellikle önerilen formülü kullanmak açıkça uygun değildir. Bu örnekten yeni hesaplama yönteminin avantajlarını görebilirsiniz.

Çözüm

Burada tanıtılan bükme kuvvetinin hesaplanmasına yönelik adımlar ve formüller, yalnızca sac metalin açılı bükülmesi için değil, aynı zamanda ark bükülmesi için de geçerlidir (kesin konuşmak gerekirse, ekstra büyük bir bükülme yarıçapı ile açılı bükme olarak adlandırılmalıdır). Levha yay şeklinde büküldüğünde kalıbın şeklinin özel olduğuna dikkat edilmelidir. Deformasyon bölgesinin izdüşümü hesaplanırken, basit bir formülle ifade edilemeyen teknolojik süreçte belirlenen teknolojik parametrelere göre hesaplanmalıdır.

Yay şeklinde bir kalıp tasarlarken, bükme kuvvetini hesaplamak için bu makalede tanıtılan yöntemi kullanarak tatmin edici sonuçlar elde edilebilir.